La Inteligencia Artificial ha sido testigo de un crecimiento monumental en reducir la brecha entre las capacidades de los humanos y las máquinas. Los investigadores y los entusiastas trabajan en numerosos aspectos en el campo para hacer que sucedan cosas asombrosas. Una de las muchas áreas es el dominio de la Visión Artificial.
La agenda de este campo es permitir que las máquinas vean el mundo como lo hacen los humanos, percibirlo en una forma similar e incluso usar el conocimiento para una multitud de tareas como el reconocimiento de Imagen y Video, Análisis y Clasificación de Imagen, Recreación Mediática, Sistemas de Recomendaciones, Procesamiento Natural del Lenguaje, etc. Los avances en la Visión Artificial con el Deep Learning han sido construídos y perfeccionados con tiempo, sobre todo con un algoritmo en particular: la Red Neuronal Convolucional (Convolutional Neural Network).
¿Listo para intentar tus propias redes neuronales convolucionales? Revisa Saturn Cloud para tener cálculos gratuitos (incluyendo GPUs gratuitos).
¿a?
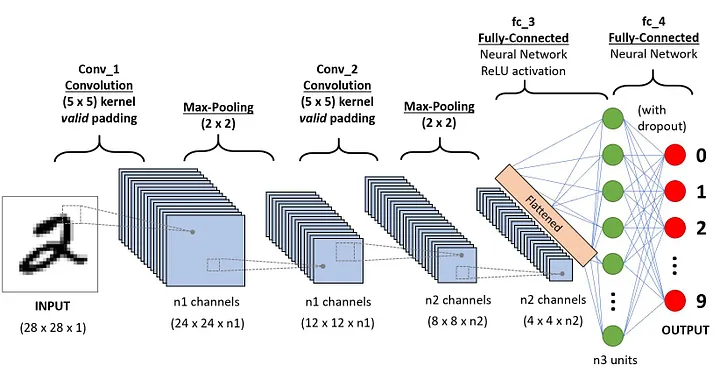
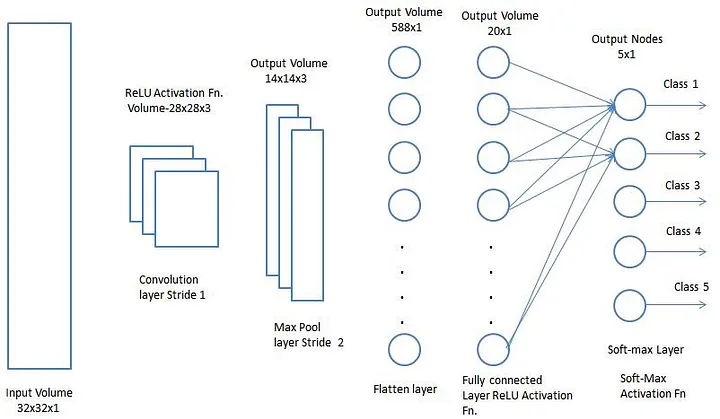
Una secuencia CNN para clasificar los dígitos hechos a mano
Una Red Neuronal Convolucional (ConvNet/CNN) es un algoritmo Deep Learning que puede tomar una imagen como entrada, asignarle importancia (pesos y sesgos de aprendizaje) a varios objetos/aspectos en la imagen y ser capaz de diferenciarlos uno del otro. El pre procesado requerido en un ConvNet es mucho más bajo comparado con otros algoritmos de clasificación. Mientras que en los métodos primitivos los filtros son diseñados a mano, con suficiente entrenamiento, los ConvNets tienen la habilidad para aprender estos filtros/características.
La arquitectura de un ConvNet es análoga al patrón de conectividad de las Neuronas en el Cerebro Humano y fue inspirado por la organización de la Corteza Visual. Las neuronas individuales sólo responden a los estímulos en una región restringida del campo visual conocido como el Campo Receptor. Una colección de estos campos superpuestos para cubrir toda el área visual.
¿Por qué ConvNets sobre las Redes Neuronales Prealimentadas?
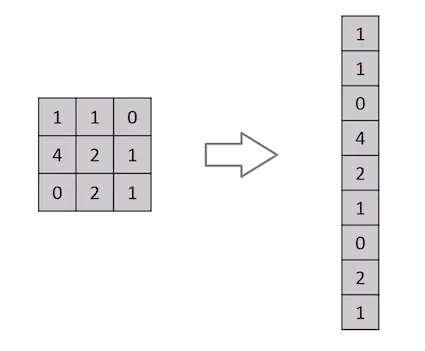
Aplanado de una matriz de imagen 3x3 en un vector 9x1
Una imagen no es nada sino una matriz de valores de píxeles, ¿verdad? Así que, ¿por qué no aplanar la imagen (por ejemplo, la matriz de una imagen 3x3 a un vector 9x1) y alimentarla a un Perceptrón Multipropósito para propósitos de clasificación? Uh… no realmente.
En casos de imágenes binarias extremadamente básicas, el método puede que muestre una puntuación de precisión promedio mientras realiza predicciones de clases pero tiene poca a ninguna precisión cuando es sobre imágenes complejas que tienen dependencias de píxeles en todo.
Un ConvNet es capaz de capturar con éxito las dependencias Espaciales y Temporales de una imagen a través de la aplicación de filtros relevantes. La arquitectura realiza un mejor ajuste al conjunto de imágenes por la reducción del número de parámetros involucrados y la reusabilidad de los pesos. En otras palabras: la red puede ser entrenada para que entienda mucho mejor la sofisticación de la imagen.
Imagen de Entrada
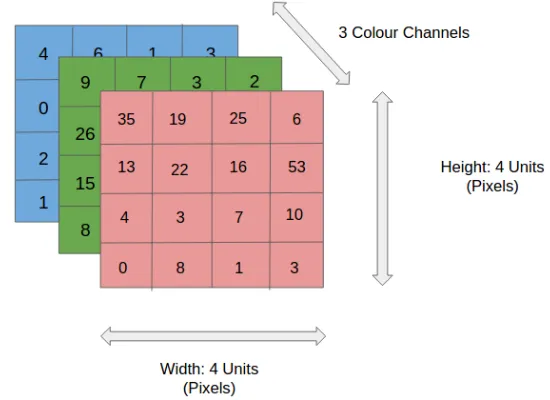
Imagen RGB 4x4x3
En la figura, tenemos una imagen RGB que ha sido separada por sus tres planos de color: rojo, verde y azul. Hay un número de tales espacios de color en las que existen imágenes: escalas de gris, RGB, HSV, CMYK, etc.
Puedes imaginar cómo las cosas se pueden volver algorítmicamente intensas una vez que las imágenes llegan a ciertas dimensiones, digamos 8k (7680x4230). El rol de ConvNet es reducir las imágenes a una forma que es fácil de procesar, sin perder las mejoras que son importantes para obtener una buena predicción. Esto es importante cuando vamos a diseñar una arquitectura que no sólo es buena en aprender mejoras pero también es escalable con conjuntos de datos masivos.
Capa Convolucional: El Kernel
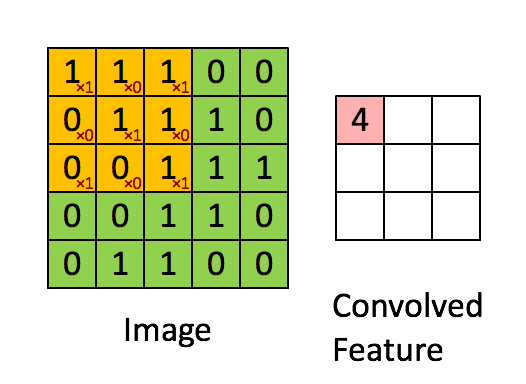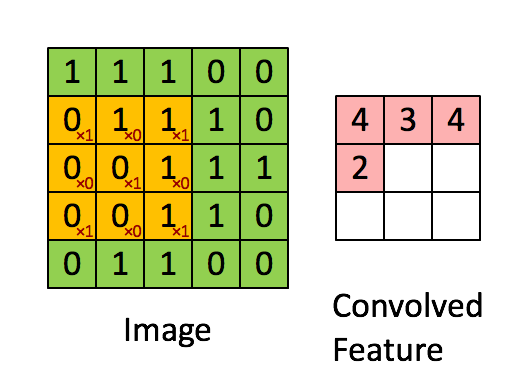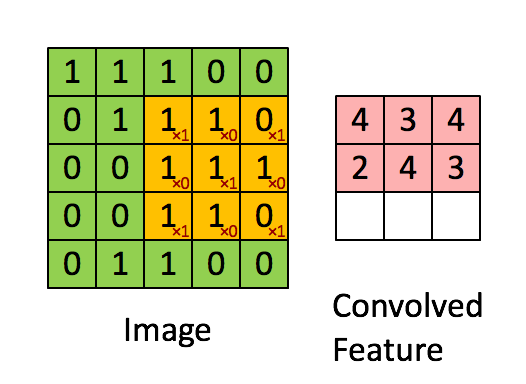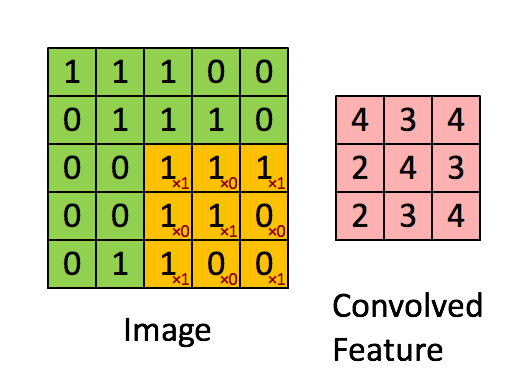
Convolucionar una imagen 5x5x1 con un kernel 3x3x1 para obtener una mejora convolucionada
Dimensiones de la imagen: 5(altura) x 5(ancho) x 1(Número de canales, es decir: RGB)
En la demostración de arriba, la sección verde recuerda nuestra imagen 5x5x1 de entrada, I. El elemento implicado en la operación de la convolución en la primera parte de la Capa Convolucional es llamada Kernel/Filtro, K, representada con el color amarillo. Hemos seleccionado K como una matriz 3x3x1.
Kernel/Filter, K =
1 0 1
0 1 0
1 0 1
El Kernel cambia 9 veces por la Longitud del Stride (Stride Length) = 1 (Sin el Stride), cada vez que realiza una operación de multiplicación elementwise (Producto Hadamard) entre K y la porción P de la imagen sobre la cual el kernel está flotando.
Movimiento del Kernel
El filtro se mueve a la derecha con ciertos Valores Stride hasta que parsea la anchura completa. Continuando, salta hacia abajo al principio (izquierda) de la imagen con el mismo Valor Stride y repite el proceso hasta que toda la imagen es atravesada.
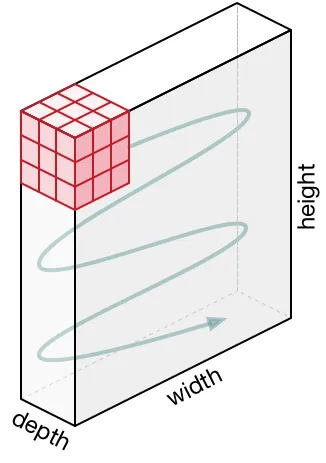
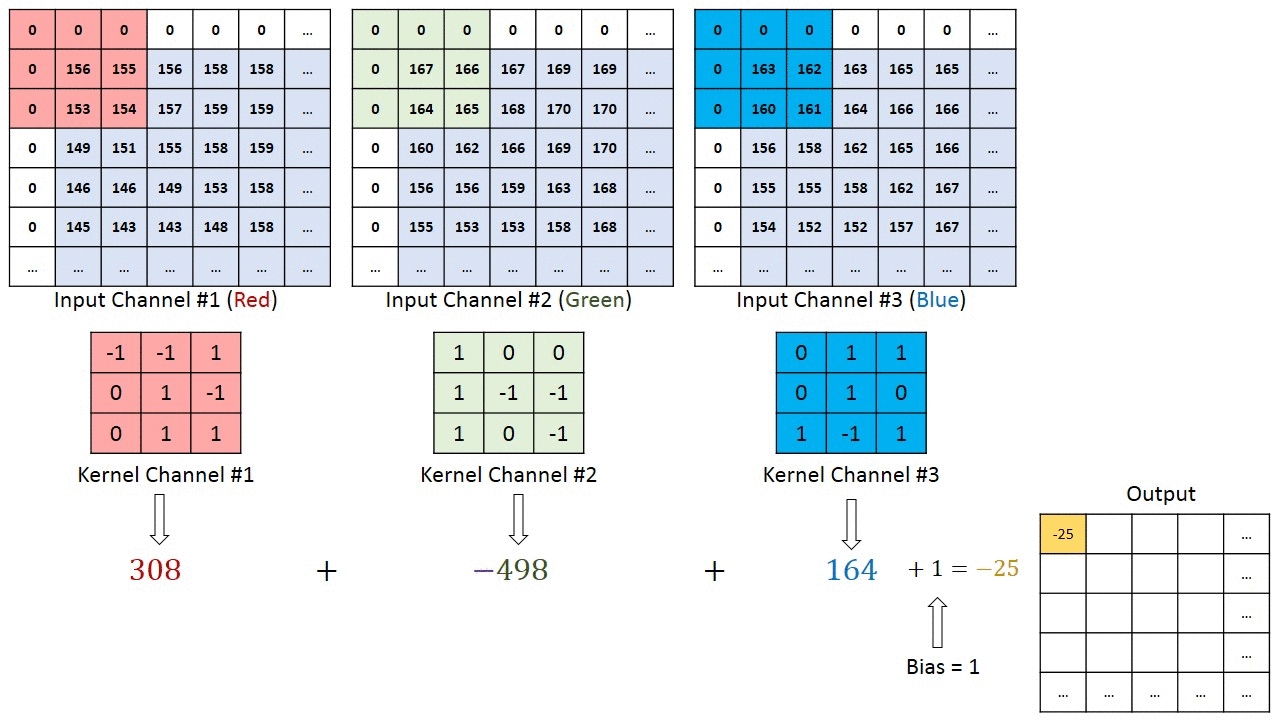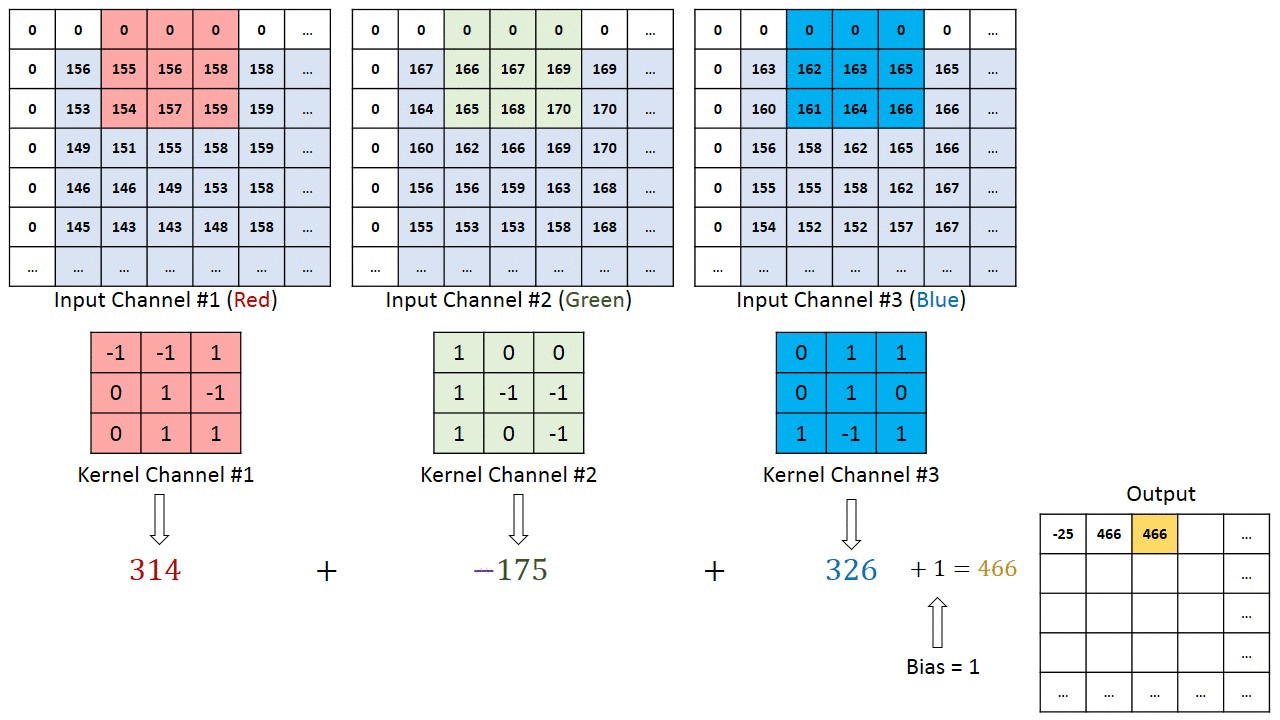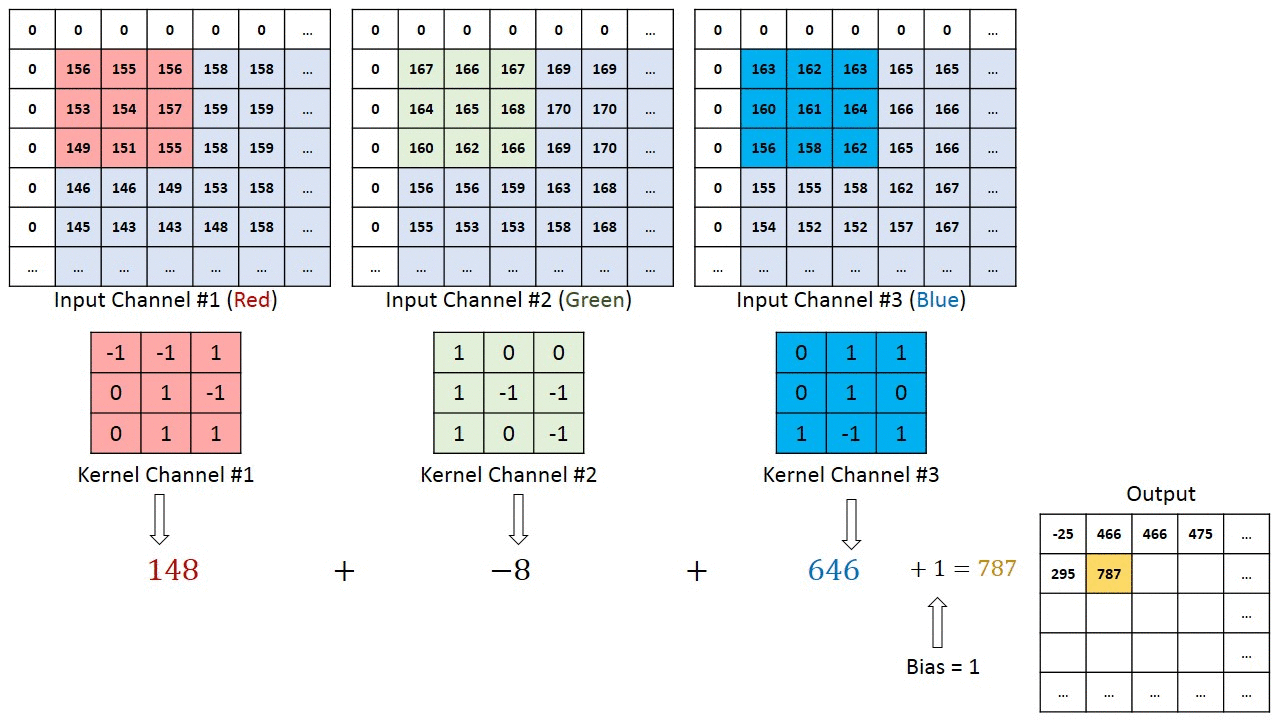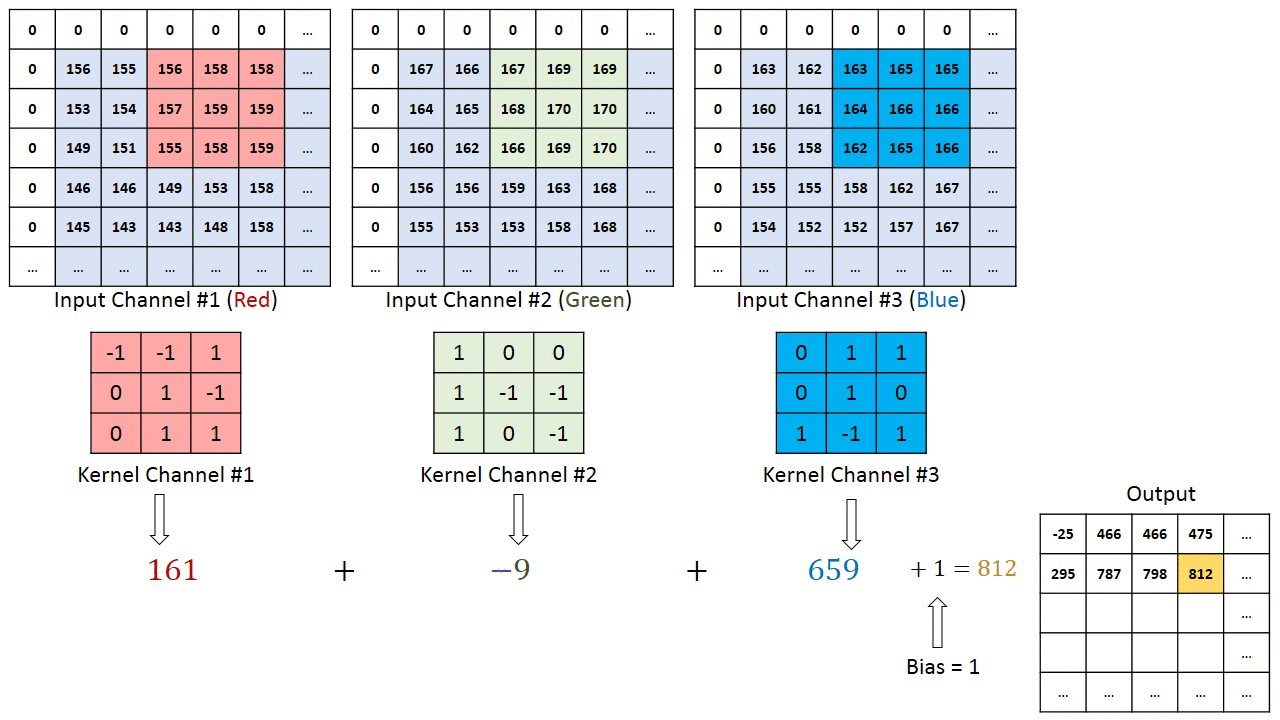
Operación de Convolución en una imagen matriz MxNx3 con un Kernel 3x3x3
En el caso de las imágenes con múltiples canales (por ejemplo: RGB), el Kernel tiene la misma profundidad que el de la imagen de entrada. La Multiplicación de la Matriz se realiza entre Kn y la pila In ([K1, I1]; [K2, I2]; [K3, I3]) y todos los resultados son sumados con el sesgo para darnos una salida de función enrevesada del canal de una profundidad aplanada.
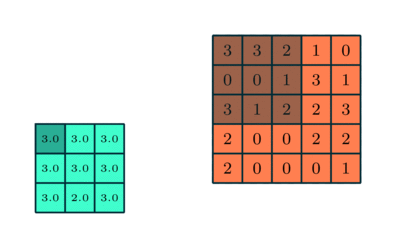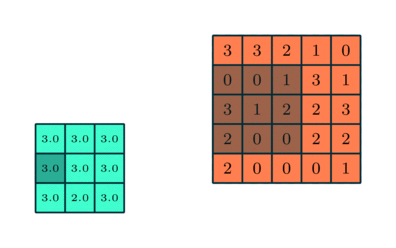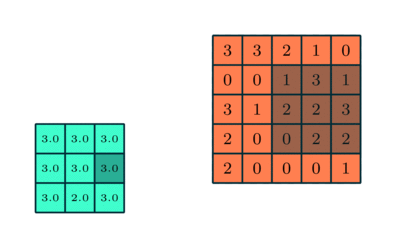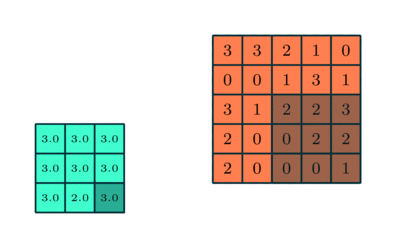
Operación de Convolución con la Longitud Stride = 2
El objetivo de la Operación Convolución es extraer las características de alto nivel como los bordes, desde la imagen de entrada. ConvNets necesita que no sea limitado a solo una Capa Convolucional. Convencionalmente, la primera capa Conv es responsable por capturar las características de Bajo Nivel como los bordes, color, orientación del gradiente, etc. Con las capas añadidas, la arquitectura se adapta a las características de Alto Nivel, dándonos una red que tiene un buen entendimiento del conjunto de datos de imagen, similar a como nosotros lo haríamos.
Hay dos tipos de resultados a la operación: una en la cual la característica convolucionada es reducida en la dimensionalidad cómo se compara en la entrada, y los otros en donde la dimensionalidad es o incrementada o permanece igual. Esto es hecho aplicando Valid Padding en el caso del anterior o Same Padding en el caso del último.
SAME padding: la imagen es “padded” con 0s para crear una imagen 6x6x1
Cuando aumentamos la imagen 5x5x1 y la imagen 6x6x1 y luego aplicamos el kernel 3x3x1 sobre ella, encontramos que la matriz convolucionada resulta ser de dimensiones 5x5x1. Por eso el mismo nombre: Same Padding.
Por su contraparte, si realizamos la misma operación sin hacer el padding, nos presentan con una matriz que tiene dimensiones en el Kernel en sí mismo (3x3x1), Valid Padding.
El siguiente repositorio contiene muchos GIFs los cuales te ayudarán a tener un mejor entendimiento sobre cómo la longitud del Padding y Stride trabajan juntos para lograr resultados relevantes para nuestras necesidades.
Capa del Pool
3x3 Pooling sobre una característica 5x5 convolucionada
Similar a la Capa Convolucional, la capa Pooling es responsable por reducir el tamaño espacial en la Característica Convolucionada. Esto es para reducir el poder algorítmico para procesar los datos a través de la reducción de la dimensionalidad. Además, es útil para extraer características dominantes los cuales son rotacionales y posicionales invariantes, manteniendo el proceso de efectivamente entrenar el modelo.
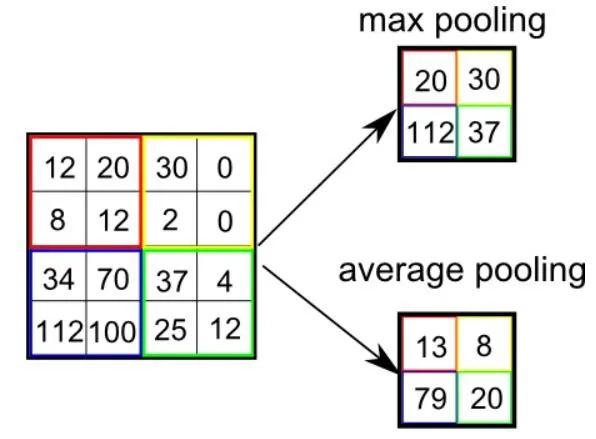
Hay dos tipos de Pooling: Pooling Máximo y Pooling Promedio, retorna el valor promedio desde la porción de la imagen cubierta por el Kernel. Por otro lado, el Pooling Promedio regresa el promedio de todos los valores desde la porción de la imagen cubierto por el Kernel.
El Pooling Máximo también realiza un Silenciador de Ruido. Descarta las activaciones ruidosas por completo y también realiza la eliminación de ruido (de-noise) junto a la reducción de la dimensionalidad. Por otro lado, entre el Pooling Promedio simplemente realiza la reducción de dimensionalidad como un mecanismo para silenciar el ruido. Por lo tanto, podemos decir que el Pooling Máximo funciona mucho mejor que el Pooling Promedio.
Tipos de Pooling
Ambos, la Capa Convolucional y la Capa Pooling, forman la capa i-th de una Red Neuronal Convolucional. Dependiendo de las complejidades de la imagen, el número de esas capas puede que se incremente para capturar aún más detalles de bajo nivel, pero con el costo de más poder algorítmico.
Después de hacer el proceso de arriba, hemos habilitado exitosamente el modelo para entender las características. En seguida, vamos a aplanar la salida final y alimentarla a la Red Neuronal regular para propósitos de clasificación.
Clasificación: Capa Totalmente Conectada (Fully Connected Layer, FC Layer)
Añadiendo una capa Totalmente Conectada es (usualmente) una forma barata de aprender combinaciones no lineales con las características de alto nivel como representado por la salida de la capa convolucional. La capa Totalmente Conectada es aprender una función no lineal de aprendizaje en ese espacio.
Ahora que hemos convertido nuestra imagen de entrada en una forma adecuada para un Perceptrón de Multi Nivel, vamos a aplanar la imagen en el vector de la columna. La salida aplanada es alimentada a una red neuronal de pre alimentación y la retropropagación se aplica a cada iteración de entrenamiento. En una serie de epochs, el modelo es capaz de distinguir entre dominar y ciertas características de bajo nivel en imágenes y clasificarlos usando la técnica de Clasificación Softmax.
Hay varias arquitecturas CNNs disponibles las cuales son claves en construir algoritmos los cuales dan poder y empoderan las IA como todo en el futuro cercano. Alguno de ellos están enumerados a continuación:
- LeNet
- AlexNet
- VGGNet
- GoogLeNet
- ResNet
- ZFNet
GitHub Notebook: Reconociendo los Dígitos Escritos a Mano usando el Conjunto de datos MNIST con TensorFlow
¿Listo para intentar tus propias redes neuronales convolucionales? Revisa Saturn Cloud para tener cálculos gratuitos (incluyendo GPUs gratuitos).
Este artículo es una traducción de Sumit Saha, hecha por Héctor Botero. Puedes encontrar el artículo original aquí.
Sería genial escucharte en nuestro Discord, puedes contarnos tus ideas, comentarios, sugerencias y dejarnos saber lo que necesitas.
Si prefieres puedes escribirnos a @web3dev_es en Twitter.








Discussion (0)