Este artículo es un intento para entender y explicar las diferencias entre la biblioteca de FixedPointMathLib de Solady y la bilbioteca Consulta ABDKMath64x64 de ABDK para Solidity, así como sus casos de uso. Únete a esta exploración y empodera tu desarrollo de Solidity con conocimientos entre elegir la biblioteca correcta para tus proyectos blockchain.
Con un entendimiento razonable de cómo funciona la biblioteca de FixedPointMathLib, es tiempo de explorar ABDKMath64x64, otra biblioteca poderosa para trabajar con los números de puntos fijos en Solidity. Puedes entender el código para la biblioteca aquí) en GitHub.
Esta biblioteca empodera a los desarrolladores para que realicen operaciones aritméticas básicas así como funciones matemáticas más avanzadas como los logaritmos, promedios, raíces cuadradas, exponenciales y más. Opera con dos números de puntos fijos int128 y regresa el resultado como un int256, eliminando el riesgo de sobreflujo. Sin embargo, el resultado va más allá del rango de ±2¹²⁸, no puede entrar dentro de la representación 64.64bit, y la operación fallará.
En este contexto, un número bit de punto fijo firmado 64.64 es, esencialmente, una fracción con un integral 128bit firmado, como el numerador y el denominador fijado de 2⁶⁴. Como el denominador se mantiene constante, no hay necesidad de almacenarlo. Consecuentemente, los números de puntos fijados firmados como 64.64bit, son representados como int128, sólo manteniendo el numerador. Así es cómo el número 64.64bit es conceptualmente estructurado:
- Los 64 bits antes del punto representa el numerador.
- Los 64 bits luego del punto representa el denominador.
Estos números ofrecen un gran rango con precisión respetable, haciéndolos adecuados para las aplicaciones que piden cálculos de números reales acertados. Usar la representación binaria también permite operaciones bit-shift, permitiendo la manipulación de datos extensivos con el costo de complejidad añadida.
Todo el int128 es usado para representar el número, y el punto separador es conceptual. El valor se deja cambiado por 2⁶⁴ en el código por los cálculos reales.
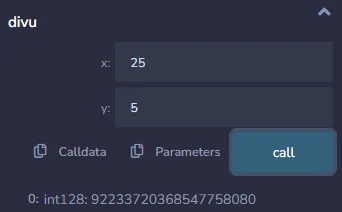
Por ejemplo, el valor 5 no es representado por el decimal familiar 5. En vez aparece como 0x00000000000000050000000000000000, el cual es equivalente a 92233720368547758080 (5* 2⁶⁴) en el formato decimal. Los primeros 16 bytes (64 bits) contienen el numerador, mientras el resto de los 16 bytes (64 bits) representan el denominador.
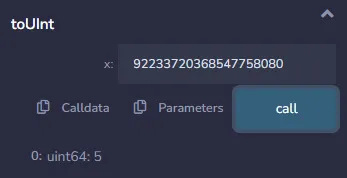
Si queremos asegurarnos tener el valor decimal, podemos usar la función toUint() desde la misma biblioteca para convertirla de vuelta.
- Los números excedentes 2⁶⁴ no pueden ser directamente representados como el punto fijo 64.64 bit.
-
Las cantidades de token deberían ser representados
uint256, no en el formato de punto fijo 64.64bit.
Casos de Uso
Hay escenarios donde la matemática fraccional es crucial cuando se trata de los valores monetarios o activos. Algunos casos de uso pueden incluir:
Cálculos de la tasa de interés: cuando trabajas con la tasa de interés, usualmente necesitas los números fraccionados. Por ejemplo: si estás calculando el interés compuesto, puede que necesites multiplicar la cantidad principal por una tasa de interés fraccionada varias veces.
Economía token: en general, los tokenomics usualmente necesitan dividir una cantidad monetaria por otra para calcular las tasas o porcentajes. Por ejemplo: necesitas calcular el porcentaje de tokens totales que cierta cuenta mantiene, lo cual conlleva dividir los números de tokens que la cuenta mantiene por el número total de tokens.
Juegos: puede que hayan juegos donde los cálculos matemáticos precisos pueden que hagan la diferencia entre un ganador y un perdedor. Los juegos con un concepto similar a NFTA.pl puede que encuentre ABDKMath64x64 para que sea una biblioteca valuable para incorporar ya que ayudaría a determinar quién está más cerca del precio, bien sea por debajo o por encima del precio.
La biblioteca ABDKMath64x64 ofrece funciones específicas para estos escenarios con funciones como muli y mulu para multiplicaciones, y divi y divu para las divisiones (con “u” denotando uint e “i” denotando int como las entradas para la función de llamada).
Diferencias Claves
La diferencia principal entre las bibliotecas ABDKMath64x64 y FixedPointMathLib recae en las representaciones del número. El primero usa números 2⁶⁴ con precisión mientras que el último usa números decimales.
Adicionalmente, ABDKMath64x64 carece de las funciones de redondeo, pero ofrece el redondeo bajo cero, además de redondear para abajo. Redondear bajo cero es un método de redondear números donde la parte fraccionada del número se remueve, efectivamente redondeando el número cerca de cero. Por ejemplo, si redondeas 2.7 cerca de cero, obtenemos 2, y si redondeas -2.7 cerca de cero, obtienes -2. Por su contraparte, si redondeas -2.7 para arriba, obtienes 3, y si redondeas -2.7, obtienes -3.
Esto puede ser beneficial en ciertas situaciones donde quieres evadir los errores de redondeo que pueden resultar en un número que es redondeado para arriba cuando debería ser redondeado para abajo, o viceversa.
Algunas otras diferencias notables entre las bibliotecas pueden incluir:
Versatilidad de las funciones: ABDKMath64x64 ofrece un gran rango de las funciones matemáticas, incluyendo la suma, resta, multiplicación, división, valor absoluto, poder, raíz cuadrada y más. Esta versatilidad se adapta a diversas operaciones matemáticas para la descentralización. Aún así, FixedPointMathLib ofrece cerca del doble de la cantidad de funciones para ejecutar, así que tiene un mayor rango de casos de uso.
Apoyo para el 64.64bit de punto fijo: ABDKMath64x64 apoya operaciones con números de puntos fijo 64.64bit, combinándolos con un gran rango con buena precisión y performance, haciéndolo ideal para aplicaciones que lidian con números reales. En contraste, el FixedPointMathLib está diseñado para trabajar con números decimales.
Eficiencia de Gas: ya que el nivel bajo de la manipulación de los datos y el casting frecuente dentro de la biblioteca, la biblioteca ABDKMath64x64 es un poco menos eficiente con el gas que FixedPointMathLib. Aquí están los costos de gas por el la misma multiplicación básica hecha por cada biblioteca:
Como se nota, el costo de la multiplicación con el ADBKMath64x64 es 78 unidades de gas más cara que con FixedPointMathLib.
Conclusión
La elección entre estas bibliotecas debería depender en las necesidades específicas de tu caso de uso. ABDKMath64x64 puede que sea más eficiente con el gas que otras muchas bibliotecas que están por allí, pero no es una mejor elección cuando se compara con FixedPointMathLib. Esto puede ser una ventaja significativa en situaciones donde la eficiencia de gas es un factor crítico.
Sin embargo, también necesitas considerar el tipo de números con los que trabajas y las operaciones que necesitas realizar. ABDKMath64x64 usa números binarios, los cuales pueden añadir complejidad innecesaria a algunos proyectos. Si tu trabajo conlleva, principalmente, números decimales, FixedPointMathLib puede que sea más adecuado.
FixedPointMathLib, con sus conjuntos de funciones sustanciales y enfocarse en los números decimales, se acomoda con un gran rango de aplicaciones. ABDKMath64x64, con su manejo de números binarios y la precisión, se adapta a proyectos en los que la precisión es primordial. La elección entre estas bibliotecas se reduce a los requisitos específicos de tu proyecto, subrayando la necesidad de un entendimiento profundo de ambos.
Ahora, si tuviese que elegir entre ambas dado por su alto rango de casos de uso, la notación fácil amigable con el usuario y la efectividad del costo, elegiría el FixedPointMathLib de Solady.
Si encontraste este artículo útil, siéntete libre para mostrar tu apoyo a través de una donación de mi dirección o a través de Kofi:
- 0x1f7972a40f8129a311e6c6a089f87347adc0e244
- https://ko-fi.com/juanxavier
¡Tu contribución es grandemente apreciada!
Este artículo es una traducción de Juan Xavier Valverde, hecha por Gabriella Martínez. Puedes encontrar el artículo original aquí
Sería genial escucharte en nuestro Discord, puedes contarnos tus ideas, comentarios, sugerencias y dejarnos saber lo que necesitas.
Si prefieres puedes escribirnos a @web3dev_es en Twitter.









Discussion (0)